Propiedades de las bisectrices de los ángulos interiores del triangulo

TEOREMA DE LAS DIRECTRICES DE LOS ÁNGULOS INTERIORES DE UN TRIÁNGULO

Funciones trigonométricas, el triangulo

Funciones trigonométricas de el triangulo

Fuente Matemática 3 de Tapia

LA PARÁBOLA TEOREMA

TEOREMA DE LA PARÁBOLA

FUNCIONES TRIGONOMÉTRICA, TRIANGULO

FUNCIÓN TRIGONOMÉTRICA DE UN TRIÁNGULO

Teorema de Rotación de ejes coordenados

Teorema de Rotación de ejes coordenados

Para simplificar las ecuaciones por rotación de ejes coordenados, necesitamos el siguiente Teorema:

Teorema 2      Si los ejes coordenados giran un ángulo f en torno de su origen como centro de rotación, y las coordenadas de un punto cualquiera P antes y después de la rotación son (X , Y) y (X´, Y´), respectivamente, las ecuaciones de transformación del sistema original al nuevo sistema de coordenadas están dadas por

                       X= X´cos & - Y´sen &
                       Y = X´sen & + Y´cos &
Demostración: Sean en la figura X y Y los ejes originales y X´y Y´los nuevos ejes. Desde el punto P tracemos la ordenada AP correspondiente al sistema X,Y , la ordenada A´P correspondiente al sistema X´, Y´y la recta 0P . Sea el ángulo P0A´= f y 0P =r Por trigonometría tenemos
                              X = 0A = r cos (&+f)                             (1)
                              Y = AP =r sen (& + f)                            (2)
                              X´= 0A´= r cos f,  Y´= A´P = r sen &    (3)
tenemos que

               X= r cos (& +f) = r cos & cos f - r sen & sen f
Si en esta última ecuación sustituimos los valores dados por (3)
obtenemos la primera ecuación de transformación,
                     X 0 X´cos & - sen &
análogamente, de (2)

               Y 0 sen (& + f) = r sen & cos f + r cos & sen f
por lo tanto, de (3) tenemos la segunda ecuación de transformación
                      Y 0 X´sen & + Y´cos &

Área de los arcos

Área de los arcos

Teorema de traslación de ejes coordenados

Teorema

Si se trasladan los ejes coordenados a un nuevo origen (y(h,k) y si las coordenadas de cualquier punto P antes y después de la traslación son (x,y) y (x´, y´), respectivamente, las ecuaciones de traslación del sistema primitivo al nuevo sistema de coordenadas son:

Demostración: Sean como la figura X e Y los ejes primitivos y X´e Y´los nuevos ejes, y sean (h, k) las coordenadas del nuevo origen 0´con referencia al sistema original. Desde el punto P, trazamos perpendiculares a ambos sistemas de ejes, y prolongamos los nuevos ejes hasta que corten a los originales, tal como se ve en la figura. Usando la relación fundamental para segmentos rectilíneos dirigidos, dada tenemos, inmediatamente que

                               x = OD = 0A + AD = 0A + 0´C = h +X´

análogamente

                              Y= 0F  =  0B + BF  = 0B + 0´F =  k + Y´

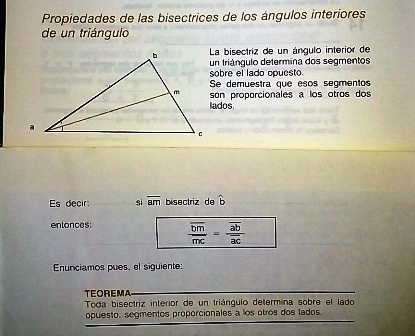
TEOREMA DE PITÁGORAS

TEOREMA DE PITÁGORAS

Este teorema puede demostrarse como una consecuencia de la propiedad de los catetos, que se ha demostrado para el triángulo rectángulo.

En efecto para cada cateto B y C se verifica:

A  =  B             A.B´  = B 2
B      B´ 

A    =  C           A.C´  =  C2

                                                                 2              2
sumando:   A. B´ + A . C´)  = B   +   C     


                                                                                 2               2
A es factor común  A ( B´ +  C´ =  B    +   C 

                                              2         2 
y B´ +  C´ =     A. A   =    B  +  C

                                             2           2
entonces          A.A    =    B  +   C

                              2               2             2
Por lo tanto        A     =    B    +  C

Que enunciamos:

EN TODO TRIÁNGULO RECTÁNGULO EL CUADRADO DE LA HIPOTENUSA ES IGUAL A LA SUMA DE LOS CUADRADOS DE LOS CATETOS

Teorema 1 simetría de la curva, teorema 2

Teorema 1 simetría de la curva

Si la ecuación de una curva no se altera cuando la variable y es reemplazada por - y, la curva es simétrica con respecto al eje X

Teorema 2

Si la ecuación de una curva no se altera cuando la variable x es reemplazada por  -x, la curva es simétrica con respecto al eje y , y recíprocamente.

Formula del volumen del cilindro

Cuerpos: La Esfera

Formula de volumen de la esfera

Cuerpos - Pirámide rectangular

Prisma

SUPERFICIE DEL CUBO

SUPERFICIE DE SEGMENTO DE CÍRCULO Y ELIPSE

SUPERFICIE DEL CIRCULO Y EL ANILLO

SUPERFICIE- AREA

FORMULAS DE SUPERFICIES

FORMULAS DE SUPERFICIE

Cuadrado     A  = a2 = lado x lado 

                     d =  a raíz cuadrada de 2

Rectángulo

Paralelogramo

Trapecio

    A   =   a  +  b   h   =    m  x  h      

                    2

     m  = a  +  b
                2

               

Triangulo

Triángulo equilátero

Pentágono

MEDIDAS Y TABLAS DE CONVERTIBILIDAD

MEDIDAS Y TABLAS DE CONVERTIBILIDAD 

MEDIDAS DE LONGITUD

KILÓMETRO    HECTÓMETRO    DECÁMETRO    METRO   DECÍMETRO  CENTÍMETRO    MILÍMETRO

         km.                    hm.                             dam.                   m.               dm.                    cm.                           mm.     

MEDIDAS DE CAPACIDAD

Kilolitro          Hectolitro         Decalitro       litro        Decilitro      Centilitro       Mililitro

      kl.                              hl.                          dal.                    l.                  dl.                          1cl.                     1ml

MEDIDAS DE PESO

Kilogramo     Hectogramo     Decagramo      Gramo     decigramo    Centigramo   miligramo

       Kg.                hg.                  dag                  g.               dg                  cg.             mg.

MEDIDAS DE SUPERFICIE

Kilómetro     Hectómetro        Decámetro       Metro      Decímetro    Centímetro      milímetro 

  cuadrado            cuadrado                 cuadrado               cuadrado       cuadrado              cuadrado                cuadrado 

    Hm2                        hm2                               dam2              m2                  dm2                         cm2                     mm2

MEDIDAS DE VOLUMEN

Kilómetro     Hectómetro        Decámetro       Metro      Decímetro    Centímetro      m ilímetro 

  cúbico                       cúbico                    cúbico                  cúbico            cúbico             cúbico                   cúbico

    Hm3                       hm3                               dam3                m3                 dm3                        cm3                     mm2

RELACIÓN ENTRE LAS UNIDADES DE VOLUMEN, CAPACIDAD Y MASA 

Un litro es la capacidad de un decímetro cúbico. • Un kilogramo es la masa que tiene el agua pura (agua destilada) que cabe en un recipiente de un decímetro cúbico de volumen. De estas dos igualdades resultan las equivalencias entre las unidades de volumen, capacidad y masa:

1 dm3 = 1litro = 1kg 

 1m3 = 1kl =  1000 litros  = 1 tonelada

1 cm3 =1 ml = 1 g 

TABLAS DE CONVERTIBILIDAD DE MEDIDAS

del sistema inglés al sistema métrico

Esta tablas son de la fuente del Manual de fórmulas técnicas de Kurt Gieck
Transformaciones del sistema inglés al sistema Métrico 

 Unidades de longitud

1 in. (pulgada)                                = 25.4 mm

1 ft.  (pié)         = 12 in.                  = 0.3048 m

1 yd. (yarda)    = 3  ft.                    =0.9144 m

1 rod. pole o perch   =5,5 yardas    =5,029  m

1 stat.mile (milla estática)              =1609,3 m

1 naut. (milla náutica)                    =1853    m

Unidades de Superficie

1 sq.in.   (pulgada cuadrada)        =6,451 cm2

1 sq. ft.   (pié cuadrado)               =0,0929 m2

1 sq.yd.   (yarda cuadrada)           =0,8361 m2

1 sq.rod, pole o perch                   =25,29   m2

1 sq.chain (cadena cuadrada)       =404,7   m2

1 ac           (acre)                           =4046,4 m2

1 sq. mile  ( milla cuadrada)         =2,59    km2

Unidades de Espacio

1 cu.in.      (pulgada cubica)         =16,39 cm3

1 cu.ft.       (pié cubico)                = 28,32 dm3

1 cu. yd.    (yarda cúbica)             = 0,7646 m3

1 imp.gallon (galón imperial)      = 4,546  l

1 US.        (galón U.S.A.)            = 3,785 l

Unidades de peso

1 drame                                       = 1,772 g

1 oz.                 (onza)                 = 28,35 p

1 lb.                  (libra)                 =0,4536 kg

1 st.               (piedra)  =14 lb.    = 6,35 kg.

1 qu.             (cuarto)  = 28 lb.    = 12,70 kg.

1 engl.cwt  (hundredweight)       = 50,80 kg

1 Us- cwt            "                       = 45,36 kg.

1 engl.ton                                    = 1,016 Mg.

1 Us-ton                                      = 0,9072 Mg

TABLAS DE CONVERTIBILIDAD DE MEDIDAS

TABLAS DE CONVERTIBILIDAD DE MEDIDAS

del sistema inglés al sistema métrico

Esta tablas son de la fuente del Manual de fórmulas técnicas de Kurt Gieck
Transformaciones del sistema inglés al sistema Métrico 

 Unidades de longitud

1 in. (pulgada)                                = 25.4 mm

1 ft.  (pié)         = 12 in.                  = 0.3048 m

1 yd. (yarda)    = 3  ft.                    =0.9144 m
1 rod. pole o perch   =5,5 yardas    =5,029  m
1 stat.mile (milla estática)              =1609,3 m
1 naut. (milla náutica)                    =1853    m

Unidades de Superficie

1 sq.in.   (pulgada cuadrada)        =6,451 cm2
1 sq. ft.   (pié cuadrado)               =0,0929 m2
1 sq.yd.   (yarda cuadrada)           =0,8361 m2
1 sq.rod, pole o perch                   =25,29   m2
1 sq.chain (cadena cuadrada)       =404,7   m2
1 ac           (acre)                           =4046,4 m2
1 sq. mile  ( milla cuadrada)         =2,59    km2

Unidades de Espacio

1 cu.in.      (pulgada cubica)         =16,39 cm3
1 cu.ft.       (pié cubico)                = 28,32 dm3
1 cu. yd.    (yarda cúbica)             = 0,7646 m3
1 imp.gallon (galón imperial)      = 4,546  l
1 US.        (galón U.S.A.)            = 3,785 l

Unidades de peso

1 drame                                       = 1,772 g
1 oz.                 (onza)                 = 28,35 p
1 lb.                  (libra)                 =0,4536 kg
1 st.               (piedra)  =14 lb.    = 6,35 kg.
1 qu.             (cuarto)  = 28 lb.    = 12,70 kg.
1 engl.cwt  (hundredweight)       = 50,80 kg
1 Us- cwt            "                       = 45,36 kg.
1 engl.ton                                    = 1,016 Mg.
1 Us-ton                                      = 0,9072 Mg

Unidades de Potencia

1 BTU/s                                  = 0,252 Kcal/m3
1 BTU/1b                              = 1,014 cv